Bài viết này chúng ta cùng ôn lại công thức tính khoảng cách giữa 2 điểm, từ điểm tới đường thẳng, qua đó vận dụng giải một số bài tập minh họa để các em hiểu rõ cách vận dụng công thức tính này với mobitool nhé !

Công thức tính khoảng cách giữa 2 điểm
Cho điểm A(xA; yA) và điểm B(xB; yB), khoảng cách giữa hai điểm này là:
Tính khoảng cách giữa 2 điểm tọa độ
– Cho đường thẳng Δ: Ax + By + C = 0 và điểm M0(x0; y0). Khi đó khoảng cách từ điểm M0 đến đường thẳng Δ là:
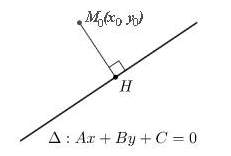
– Khoảng cách từ điểm M0 đến đường thẳng Δ là độ dài của đoạn thẳng M0H (trong đó H là hình chiếu vuông góc của M0 lên Δ).
Lưu ý: Trong trường hợp đường thẳng Δ chưa viết dưới dạng tổng quát thì đầu tiên ta cần đưa đường thẳng Δ về dạng tổng quát.
Cách tính khoảng cách giữa 2 điểm từ điểm tới đường thẳng qua bài tập minh họa
* Ví dụ 1: Trong mặt phẳng Oxy cho điểm A(1;2) và điểm B(-3;4). Tính độ dài đoạn thẳng AB.
* Lời giải:
– Độ dài đoạn thẳng AB là khoảng cách giữa 2 điểm A,B ta có:
* Ví dụ 2: Tính khoảng cách từ điểm M(2;-1) đến đường thẳng (Δ): 3x + 4y + 7 = 0.
* Lời giải:
– Khoảng cách từ điểm M đến đường thẳng (Δ) là:
* Ví dụ 3: Tính khoảng cách từ điểm A(0;1) đến đường thẳng (Δ): 4x + 3y = 6
* Lời giải:
– Đường thẳng (Δ): 4x + 3y = 6 ⇔ 4x + 3y – 6 = 0
– Khoảng cách từ điểm A đến (Δ) là:
* Ví dụ 4: Tính khoảng cách từ điểm M(1;1) đến đường thẳng (Δ) có phương trình tham số: x = 3 + 3t và y = 2 + t.
* Lời giải:
– Ta cần đưa phương trình đường thẳng (Δ) về dạng tổng quát.
– Ta có: (Δ) đi qua điểm A(3;2) và có VTCP ⇒ VTPT
⇒ Phương trình (Δ): 1.(x – 3) – 3(y – 2) = 0 ⇔ x – 3y + 3 = 0
⇒ Khoảng cách từ điểm M(1;1) đến (Δ) là:
* Ví dụ 5: Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng (Δ): 4x – 3y + 25 = 0. Bán kính R của đường tròn (C) bằng:
* Lời giải:
– Do đường thẳng (Δ) tiếp xúc với đường tròn (C) nên khoảng cách từ tâm đường tròn đến đường thẳng (Δ) chính là bán kính R của đường tròn.
* Ví dụ 6: Khoảng cách từ giao điểm của hai đường thẳng (d1): x – 3y + 4 = 0 và(d2): 2x + 3y – 1 = 0 đến đường thẳng ∆: 3x + y + 16 = 0 bằng:
* Lời giải:
– Trước hết ta cần tìm giao điểm của (d1) và (d2); từ đó tính khoảng cách từ giao điểm này tới (∆).
– Giả sử giao điểm của (d1) và (d2) là A thì tọa độ của A là nghiệm của hệ phương trình:
x – 3y + 4 = 0 và 2x + 3y – 1 = 0
Giải hệ được x = -1 và y = 1 ⇒ A(-1;1)
– Khoảng cách từ điểm A(-1;1) đến đường thẳng ∆: 3x + y + 16 = 0 là:
* Ví dụ 7: Trong mặt phẳng hệ tọa độ Oxy, cho tam giác ABC có A(1;1); B(0;3) và C(4;0).
a) Tính chiều dài đường cao AH (H thuộc BC).
b) Tính diện tích tam giác ABC
* Lời giải:
a) Tính chiều dài đường cao AH
– Chiều dài đường cao AH chính là khoảng cách từ A tới đường thẳng BC. Vì vậy ta cần viết phương trình dường thẳng BC từ đó tính khoảng cách từ A tới BC.
– PT đường thẳng BC: Đi qua B(0;3) và có CTCP BC(xC – xB; yC – yB) = (4;-3) nên VTPT là n(3;4).
⇒ PTĐT (BC) là: 3(x – 0) + 4( y – 3) = 0 ⇔ 3x + 4y – 12 = 0
⇒ chiều cao của tam giác kẻ từ đỉnh A chính là khoảng cách từ điểm A đến đường thẳng BC:
b) Tính diện tích tam giác ABC.
– Ta có: SΔABC = (1/2).AH.BC
– Có độ dài BC là:
– Mà AH = d(A;BC) = 1 (theo câu a)
⇒ SΔABC = (1/2)mobitool.net = (1/2).1.5 = 5/2 =2,5.
